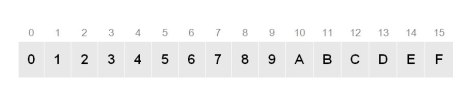
Шестнадесетичните числа

Шестнадесетична бройна система

Както всяка бройна система, шестнадесетичната също съдържа набор от символи, с които да се представят числата в нея. За разлика от десетичната система, с която сме свикнали да пресмятаме, тук се ползват освен цифрите от 0 до 9, също и няколко букви от латинската азбука: A, B, C, D, E и F, които изразяват стойности от 10 до 15.

Шестнадесетичната система е позиционна, както десетичната. Това означава, че стойността на отделната цифра зависи от мястото, на което се намира тя в рамките на дадено число.

За сравнение, римската бройна система е непозиционна. Ако вземем цифрата V, тя продължава да означава 5, когато я видим в число като VI например. Просто по правилата на римската бройна система, добавяме към V по-малката стойност на цифрата I след него, затова VI има стойност 6, а не 51. Напротив, според десетичната бройна система, която е позиционна, цифрата 5 в числото 51 обозначава десетиците, съответно нейната стойност не е 5, а 50.

Основата при шестнадесетичната бройна система е числото 16. Знаем, че за основа на дадена бройна система се приема онова число (с абсолютна стойност, различна от 0 и 1), което се равнява на броя цифри в тази система, използвани за запис на отделните числа в нея. Шестнадесетичната система използва 16 символа, за да представи записите на отделните числа. При десетичната система символите са 10 (от 0 до 9 включително).

Приложение на HEX числата

Двоичното представяне на числата е много удобно за компютърните пресмятания. За съхранение на данните в оперативната памет, се ползва двоичен код. Но въпреки, че двоичната бройна система се е наложила при компютрите, тя има и един недостатък: числата там нарастват много бързо и съответно заемат твърде много битове (разреди) в компютърната памет. Освен това, са неудобни за ползване от човека.

Шестнадесетичната система решава проблема с дългите записи, тъй като позволява да се работи по-лесно с големи числа. Изписването на числата в шестнадесетичен формат е доста по-кратко. IPv6 адресите се представят в шестнадесетичен формат, както и физическите адреси на компютрите. Записан в двоичен вид, физическият адрес би заел цели 48 бита, което би затруднило филтрирането на MAC адресите при безжичните връзки.

За обозначаване на цветовете също може да се ползва шестнадесетичен код. Код на всеки желан цвят може да генерирате от тук.

Особености на шестнадесетичния запис

Шестнадесетичните числа са поредица от цифри и (или) букви. Когато числото се състои само от цифри, пред тях се поставя идентификатор 0x, който обозначава числото като шестнадесетично, например: 0x56 не е равнозначно на десетичното число 56. Друг начин за обозначение е с индекс долу вдясно до числото, който показва бройната система, в която е числото: 56_HEX.

Всяка шестнадесетична цифра/буква се представя като група от 4 бита, със съответни двоични стойности (0 или 1) на всяка от четирите позиции. Позициите се броят отдясно-наляво, като степени на двойката от нулева до трета: 2⁰ = 1; 2¹ = 2; 2² = 4; 2³ = 8.

Примери:

Числото A_HEX има двоичен запис 1010 и десетична стойност 10, която получаваме при събиране на 8 + 2.

Числото B_HEX има двоичен запис 1010 и десетична стойност 11, която получаваме при събиране на 8 + 2 + 1.

Числото C_HEX има двоичен запис 1010 и десетична стойност 12, която получаваме при събиране на 8 + 4.

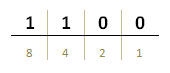
Числото D_HEX има двоичен запис 1010 и десетична стойност 13, която получаваме при събиране на 8 + 4 + 1.

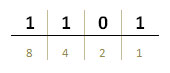
Числото E_HEX има двоичен запис 1010 и десетична стойност 14, която получаваме при събиране на 8 + 4 + 2.

Числото F_HEX има двоичен запис 1010 и десетична стойност 15, която получаваме при събиране на 8 + 4 + 2 + 1.

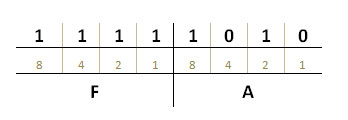
Числото FA_HEX има двоичен запис 1111 1010, където първата група битове 1111 има стойност 15 (F), а втората група битове 1010 има стойност 10 (A). Двете стойности се получават при събиране на включените битове (позициите с единица):

Преобразуване

Всяко число може да се преобразува от една бройна система в друга. Лесно можем да представяме шестнадесетичните числа в десетични, както и обратно, с помощта на двоичния им запис. За улеснение, можем да ползваме помощни таблици, както е показано по-долу, или да събираме и изваждаме степени на двойката.

Шестнадесетичен към десетичен формат

Първото, което правим с шестнадесетичното число, е да го разделим на сегменти, всеки от които да представим в двоичен вид.

Пример: C5_HEX 

Цифрата C означава десетично 12. За да я видим в двоичен вид, включваме онези битови позиции от нулева до трета, при сбора на които ще получим 12. Това означава позиция 2³ и 2², които се равняват съответно на 8 и 4. За по-бързо пресмятане в двоичен формат, можем да ползваме Помощна таблица 1. Същото правим и с цифрата 5: включваме позициите 2² и 2⁰, чиито сбор (4 + 1) ни дава стойност 5.

След като сме получили, че двоичната стойност на C5 е 1100 0101, можем да преобразуваме двоичното число в десетично. За целта, събираме стойностите на включените битови позиции отдясно-наляво, отново като степени на двойката, но този път за цялата дължина на числото, а не поотделно за сегментите му:

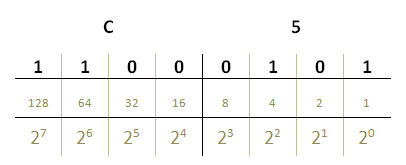
Сумата е: 2⁷ + 2⁶ + 2² + 2⁰ или 128 + 64 + 4 + 1 = 197

Пример: FF_HEX

Разделяме числото на 2 сегмента, според броя на символите в него, и го преобразуваме в двоичен формат, а след това събираме включените битове (в случая всички са включени):

Десетичен формат: 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255

За по-лесно изчисление, можем да използваме Помощна таблица 2, която ни показва десетичната стойност на сумата от поредни включени битове, броени от 8-ми към 1-ви бит:

Таблицата ни дава готова калкулация на сумата от стойностите на поредни битове (вж. колонката СУМА).

Пример: двоичното 1110 0001 съдържа три поредни включени бита на позиции 8, 7 и 6, които ни дават стойност 224, и към нея прибавяме стойността на първия бит, която е 1. По този начин получаваме, че в двоичен формат числото е 225.

Таблицата може да е от полза и при пресмятане на по-дълги двоични числа, но там се добавя и стойността на включените битове от 9-та позиция нататък. Така например, при двоичното 10 1100 1000 калкулацията е, както следва: 512 + 192 + 8 = 712 (десетично).

Десетичен към шестнадесетичен формат

Правим преобразуването от десетичен формат към шестнадесетичен също през двоичен запис.

Пример: 225 

Както видяхме от Помощна таблица 2, три поредни включени бита дават стойност 224: това са позиции 2⁷ + 2⁶ + 2⁵. За да получим десетичното 225, трябва да включим още един бит, със стойност 1 и съответна степен на двойката 2⁰.

Полученото двоично число 1110 0001 разделяме на сегменти от по 4 бита. За всеки от тях изчисляваме шестнадесетичния му еквивалент: първият сегмент 1110 е със стойност 8 + 4 + 2 = 14 (или съответно E_HEX), а вторият 0001 е със стойност 1. За тази калкулация можем да си послужим и с Помощна таблица 1.

Пример: 120

Осмата битова позиция, която е и седмата степен на двойката (2⁷ = 128) е с твърде висока стойност, по-голяма от 120. Поради това, на тази позиция поставяме 0.

Позиция седма, която е шестата степен на двойката (2⁶ = 64), е по-малка от 120, съответно там поставяме 1. Изваждаме 64 от числото: 120 – 64 = 56. Остатъкът е 56.

Позиция шеста, която е пета степен на двойката (2⁵ = 32), е по-малка от остатъка 56, съответно и там поставяме 1. Изваждаме 32 от остатъка: 56 – 32 = 24. Новият остатък е 24.

Позиция пета, която е четвърта степен на двойката (2⁴ = 16), е по-малка от остатъка 24, съответно и там поставяме 1. Изваждаме 16 от остатъка: 24 – 16 = 8. Новият остатък е 8.

Позиция четвърта, която е трета степен на двойката (2³ = 8), е равна на остатъка 8, съответно и там поставяме 1. Изваждаме 8 от остатъка: 8 – 8 = 0. Нямаме нов остатък, затова на останалите три позиции поставяме нули.

Така двоичното число, което получаваме, е 0111 1000:

Нулите от лявата страна не се броят. За да преобразуваме бинарното число в шестнадесетично, отново го разделяме на сегменти от по 4 бита, като броим отдясно-наляво:

Калкулираме стойностите на двата сегмента: 4 + 2 + 1 = 7 (от лявата страна) и 8 (от дясната страна). Шестнадесетичният запис на числото е 0x78.

Пример: 252

Виждаме от Помощна таблица 2, че 6 поредни включени бита ни дават точно числото 252: 128 + 64 + 32 + 16 + 8 + 4 = 252. Съответно, бинарният запис би бил:

Преобразуваме двоичното число в шестнадесетично:

Калкулираме стойностите на двата сегмента: 8 + 4 + 2 + 1 = 15 или F (от лявата страна) и 12 или C (от дясната страна). Шестнадесетичният запис на числото е FC.

Пример: 620

Числото 620 надвишава стойността на осмата битова позиция, която е 128. Това означава, че бинарният запис ще се простира в по-дълъг набор от битове.

На девета позиция имаме стойност 256 (2⁸), което също е по-малко от 620, затова продължаваме да разширяваме битовата редица.

На десета позиция имаме стойност 512 (2⁹), отново по-малко от 620.

На единадесета позиция стойността е 1024, което вече надхвърля числото 620. Така разбираме, че бинарният запис на нашето число ще съдържа общо 10 битови позиции:

Разширили сме записите на двойката до битовата позиция на онази степен, която по стойност е максимално голямо число, равно или съдържащо се в 620.

Стойността на десетата битова позиция 512 (2⁹) изваждаме от 620 и поставяме на тази позиция 1. Остатъкът е 620 – 512 = 108.

Стойността на деветата битова позиция 256 (2⁸) е по-малка от остатъка 108, затова на тази позиция поставяме 0.

Стойността на осмата битова позиция 128 (2⁷) също е по-малка от остатъка 108, затова и на тази позиция поставяме 0.

Стойността на седмата битова позиция 64 (2⁶) изваждаме от остатъка 108 и поставяме на тази позиция 1. Новият остатък е 108 – 64 = 44.

Стойността на шестата битова позиция 32 (2⁵) изваждаме от остатъка 44 и поставяме на тази позиция 1. Новият остатък е 44 – 32 = 12.

Стойността на петата битова позиция 16 (2⁴) е по-малка от остатъка 12, затова на тази позиция поставяме 0.

Стойността на четвъртата битова позиция 8 (2³) изваждаме от остатъка 12 и поставяме на тази позиция 1. Новият остатък е 12 – 8 = 4.

Стойността на третата битова позиция 4 (2²) изваждаме от остатъка 4 и поставяме на тази позиция 1. Новият остатък е 4 – 4 = 0.

Нямаме нов остатък, затова на останалите две позиции поставяме нули. Двоичното число, което получаваме, е: 10 0110 1100:

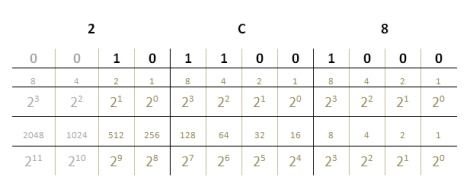
Разделяме битовете на сегменти от по 4 бита, броено отдясно-наляво и по познатия начин събираме степените на двойката в отделните сегменти, за да получим компонентите на шестнадесетичното число: 26C.

Да вземем за пример едно по-голямо бинарно число, което да обърнем в шестнадесетичен и съответно в десетичен формат.

Пример: 1001 1101 1011 0001

Дописваме редицата битови позиции от осма нататък и сегментираме двоичното число на 4 групи от по 4 бита:

Според включените битове, изчисляваме десетичния еквивалент на числото:

32 768 + 4 096 + 2 048 + 1024 + 256 + 128 + 32 + 16 + 1 = 40 369

Шестнадесетичен еквивалент: 9DB1

Източници:

• Въведение в програмирането със C# : Бройни системи
• Learn how to do Hex conversions in under 30 seconds! – Lazaro (Laz) Diaz
• The MAC Address